15  Inference for one proportion

Functions introduced in this chapter

No new R functions are introduced here.

15.1 Introduction

Our earlier work with simulations showed us that when the number of successes and failures is large enough, we can use a normal model as our sampling distribution model.

We revisit hypothesis tests for a single proportion, but now, instead of running a simulation to compute the P-value, we take the shortcut of computing the P-value directly from a normal model.

There are no new concepts here. All we are doing is revisiting the rubric for inference and making the necessary changes.

15.1.1 Install new packages

There are no new packages used in this chapter.

15.1.2 Download the Quarto file

Look at either the top (Posit Cloud) or the upper right corner of the RStudio screen to make sure you are in your intro_stats project.

Then click on the following link to download this chapter as a Quarto file (.qmd).

https://vectorposse.github.io/intro_stats/chapter_downloads/15-inference_for_one_proportion.qmd

Once the file is downloaded, move it to your project folder in RStudio and open it there.

15.1.3 Restart R and run all chunks

In RStudio, select “Restart R and Run All Chunks” from the “Run” menu.

15.2 Load packages

We load the standard tidyverse, janitor and infer packages as well as the openintro package to access data on heart transplant candidates. We’ll include mosaic for one spot below when we compare the results of infer to the results of graphing a normal distribution using qdist.

library(tidyverse)

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.4     ✔ tidyr     1.3.1
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

library(janitor)

Attaching package: 'janitor'

The following objects are masked from 'package:stats':

    chisq.test, fisher.test

library(infer)
library(openintro)

Loading required package: airports
Loading required package: cherryblossom
Loading required package: usdata

library(mosaic)

Registered S3 method overwritten by 'mosaic':
  method                           from   
  fortify.SpatialPolygonsDataFrame ggplot2

The 'mosaic' package masks several functions from core packages in order to add 
additional features.  The original behavior of these functions should not be affected by this.

Attaching package: 'mosaic'

The following object is masked from 'package:Matrix':

    mean

The following object is masked from 'package:openintro':

    dotPlot

The following objects are masked from 'package:infer':

    prop_test, t_test

The following objects are masked from 'package:dplyr':

    count, do, tally

The following object is masked from 'package:purrr':

    cross

The following object is masked from 'package:ggplot2':

    stat

The following objects are masked from 'package:stats':

    binom.test, cor, cor.test, cov, fivenum, IQR, median, prop.test,
    quantile, sd, t.test, var

The following objects are masked from 'package:base':

    max, mean, min, prod, range, sample, sum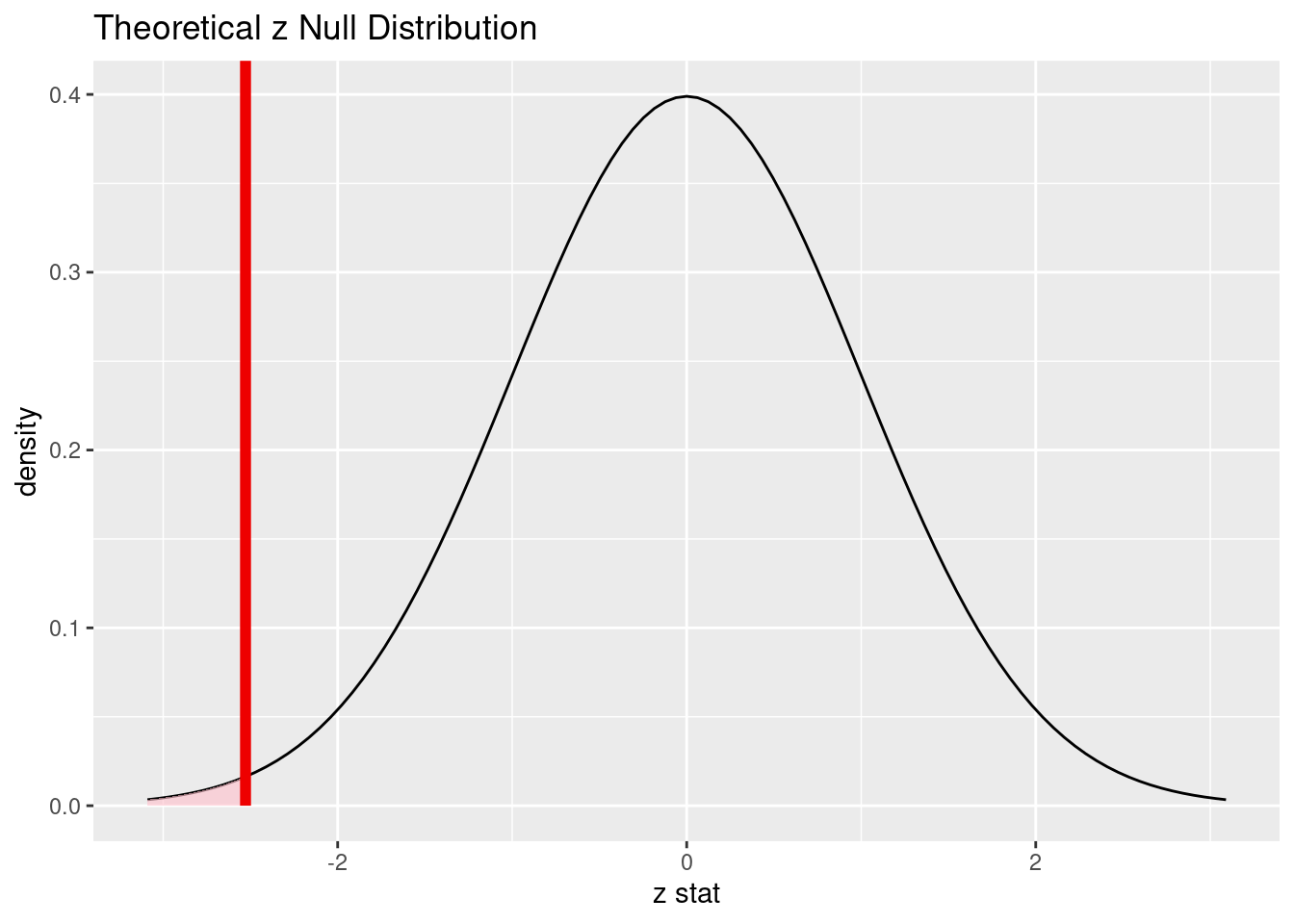

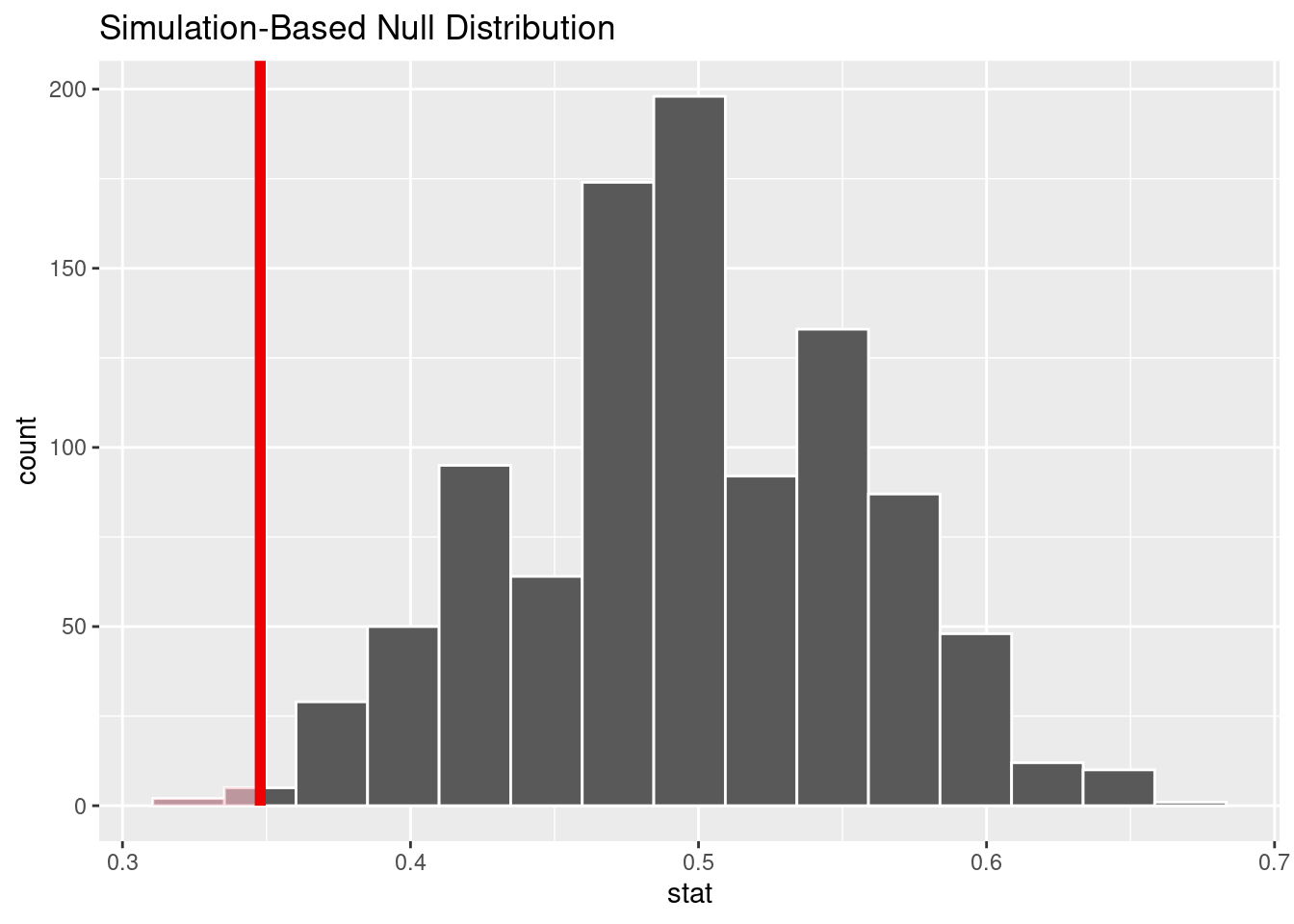
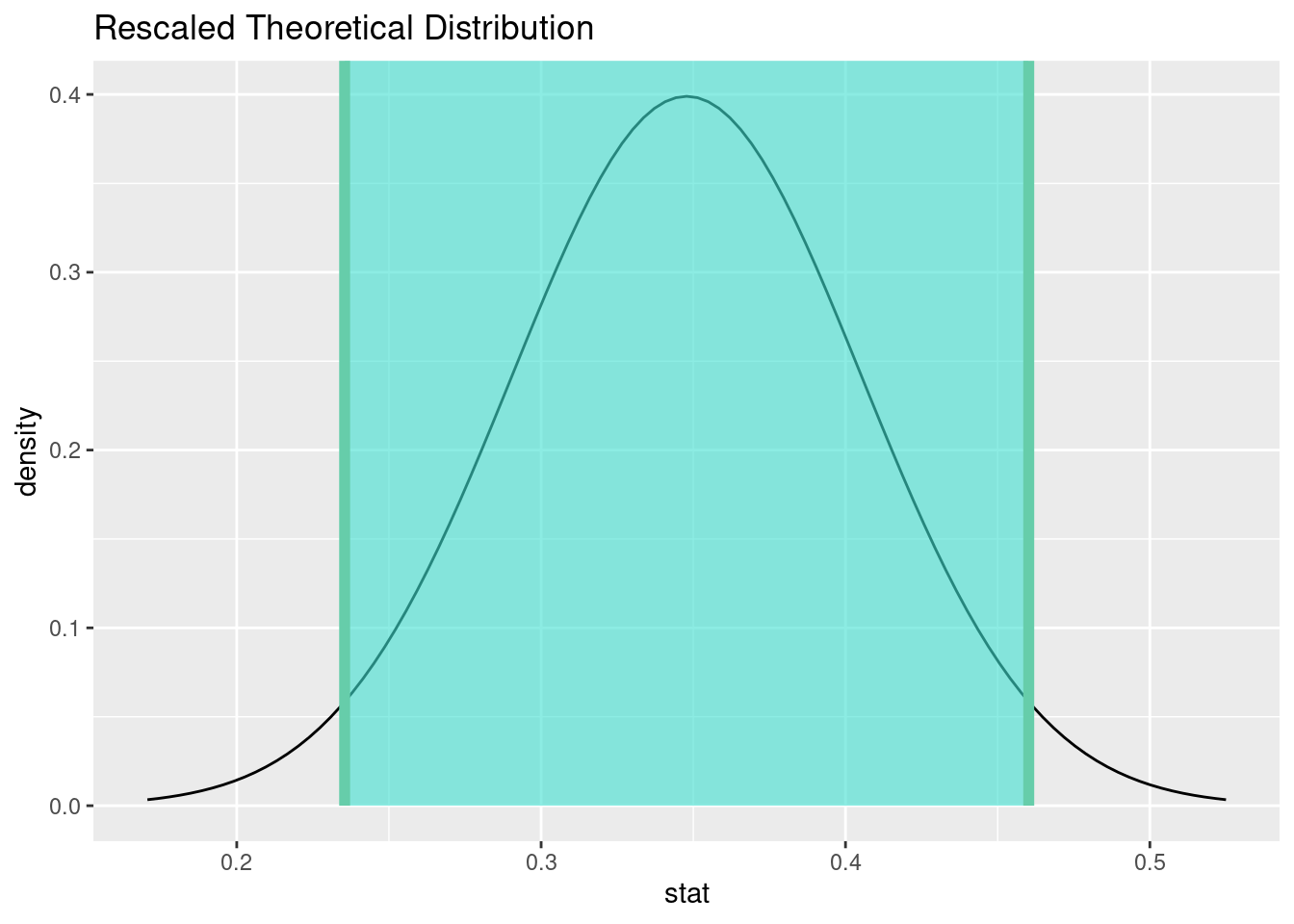
15.3 Revisiting the rubric for inference

Instead of running a simulation, we are going to assume that the sampling distribution can be modeled with a normal model as long as the conditions for using a normal model are met.

Although the rubric has not changed, the use of a normal model changes quite a bit about the way we go through the other steps. For example, we won’t have simulated values to give us a histogram of the null model. Instead, we’ll go straight to graphing a normal model. We won’t compute the percent of our simulated samples that are at least as extreme as our test statistic to get the P-value. The P-value from a normal model is found directly from shading the model.

What follows is a fully-worked example of inference for one proportion. After the hypothesis test (sometimes called a one-proportion z-test for reasons that will become clear), we also follow up by computing a confidence interval. From now on, we will consider inference to consist of a hypothesis test and a confidence interval. Whenever you’re asked a question that requires statistical inference, you should follow both the rubric steps for a hypothesis test and for a confidence interval.

The example below will pause frequently for commentary on the steps, especially where their execution will be different from what you’ve seen before when you used simulation. When it’s your turn to work through another example on your own, you should follow the outline of the rubric, but you should not copy and paste the commentary that accompanies it.

15.4 Research question

Data from the Stanford University Heart Transplant Study is located in the openintro package in a data frame called heart_transplant. From the help file we learn, “Each patient entering the program was designated officially a heart transplant candidate, meaning that he was gravely ill and would most likely benefit from a new heart.” Survival rates are not good for this population, although they are better for those who receive a heart transplant. Do heart transplant recipients still have less than a 50% chance of survival?

15.5 Exploratory data analysis

15.5.1 Use data documentation (help files, code books, Google, etc.) to determine as much as possible about the data provenance and structure.

Start by typing ?heart_transplant at the Console or searching for heart_transplant in the Help tab to read the help file.

Exercise 1

At the bottom of the help file, there is a URL listed for the “Source”. Click on this link. Is there any information about the provenance of the data at this link?

Next, look at the paper listed under “References” (a 1974 article by authors Turnbull, Brown, and Hu). How can you tell that this “reference” is not, in fact, a direct reference to a medical research article reporting on the Stanford University Heart Transplant Study?

Finally, do an internet search to find the original research article from 1974. Why is this search process also not likely to help you determine the provenance of the data?

Please write up your answer here.

---

Now that we have learned everything we can reasonably learn about the data, we print it out and look at the variables.

heart_transplant

glimpse(heart_transplant)

Rows: 103
Columns: 8
$ id         <int> 15, 43, 61, 75, 6, 42, 54, 38, 85, 2, 103, 12, 48, 102, 35,…
$ acceptyear <int> 68, 70, 71, 72, 68, 70, 71, 70, 73, 68, 67, 68, 71, 74, 70,…
$ age        <int> 53, 43, 52, 52, 54, 36, 47, 41, 47, 51, 39, 53, 56, 40, 43,…
$ survived   <fct> dead, dead, dead, dead, dead, dead, dead, dead, dead, dead,…
$ survtime   <int> 1, 2, 2, 2, 3, 3, 3, 5, 5, 6, 6, 8, 9, 11, 12, 16, 16, 16, …
$ prior      <fct> no, no, no, no, no, no, no, no, no, no, no, no, no, no, no,…
$ transplant <fct> control, control, control, control, control, control, contr…
$ wait       <int> NA, NA, NA, NA, NA, NA, NA, 5, NA, NA, NA, NA, NA, NA, NA, …

Commentary: The variable of interest is survived, which is coded as a factor variable with two categories, “alive” and “dead”. Keep in mind that because we are interested in survival rates, the “alive” condition will be considered the “success” condition.

There are 103 patients, but we are not considering all these patients. Our sample should consist of only those patients who actually received the transplant. The following table shows that only 69 patients were in the “treatment” group (meaning that they received a heart transplant).

tabyl(heart_transplant, transplant) |>
  adorn_totals()

15.5.2 Prepare the data for analysis.

First, we check for missing data:

heart_transplant |>
  drop_na(transplant) |>
  NROW()

[1] 103

Since there are still 103 rows, we have no missing data in the variable of interest.

Commentary: This is the same as we’ve done before, except that we added the NROW() command as a handy summary that just counts the number of rows.

CAUTION: If you are copying and pasting from this example to use for another research question, the following code chunk is specific to this research question and not applicable in other contexts.

We need to use filter so we get only the patients who actually received the heart transplant.

# Do not copy and paste this code for future work
heart_transplant2 <- heart_transplant |>
  filter(transplant == "treatment")
heart_transplant2

Commentary: don’t forget the double equal sign (==) that checks whether the treatment variable is equal to the value “treatment”. (See the Chapter 5 if you’ve forgotten how to use filter.) Note that this reduces the sample size to 69 for the remainder of this hypothesis test.

Again, this step isn’t something you need to do for other research questions. This question is peculiar because it asks only about patients who received a heart transplant, and that only involves a subset of the data we have in the heart_transplant data frame.

15.5.3 Make tables or plots to explore the data visually.

Making sure that we refer from now on to the heart_transplant2 data frame and not the original heart_transplant data frame:

tabyl(heart_transplant2, survived) |>
  adorn_totals()

15.6 Hypotheses

15.6.1 Identify the sample (or samples) and a reasonable population (or populations) of interest.

The sample consists of 69 heart transplant recipients in a study at Stanford University. The population of interest is presumably all heart transplants recipients.

15.6.2 Express the null and alternative hypotheses as contextually meaningful full sentences.

\(H_{0}:\) Heart transplant recipients have a 50% chance of survival.

\(H_{A}:\) Heart transplant recipients have less than a 50% chance of survival.

Commentary: It is slightly unusual that we are conducting a one-sided test. The standard default is typically a two-sided test. However, it is not for us to choose: the proposed research question is unequivocal in hypothesizing “less than 50%” survival.

15.6.3 Express the null and alternative hypotheses in symbols (when possible).

\(H_{0}: p_{alive} = 0.5\)

\(H_{A}: p_{alive} < 0.5\)

15.7 Model

15.7.1 Identify the sampling distribution model.

We will use a normal model.

Commentary: In past chapters, we have simulated the sampling distribution or applied some kind of randomization to simulate the effect of the null hypothesis. The point of this chapter is that we can—when the conditions are met—substitute a normal model to replace the unimodal and symmetric histogram that resulted from randomization and simulation.

15.7.2 Check the relevant conditions to ensure that model assumptions are met.

• Random
  • Since the 69 patients are from a study at Stanford, we do not have a random sample of all heart transplant recipients. We hope that the patients recruited to this study were physiologically similar to other heart patients so that they are a representative sample. Without more information, we have no real way of knowing.
• 10%
  • 69 patients are definitely less than 10% of all heart transplant recipients.
• Success/failure

\[ np_{alive} = 69(0.5) = 34.5 \geq 10 \]

\[ n(1 - p_{alive}) = 69(0.5) = 34.5 \geq 10 \]

Commentary: Notice something interesting here. Why did we not use the 24 patients who survived and the 45 who died as the successes and failures? In other words, why did we use \(np_{alive}\) and \(n(1 - p_{alive})\) instead of \(n \hat{p}_{alive}\) and \(n(1 - \hat{p}_{alive})\)?

Remember the logic of inference and the philosophy of the null hypothesis. To convince the skeptics, we must assume the null hypothesis throughout the process. It’s only after we present sufficient evidence that can we reject the null and fall back on the alternative hypothesis that encapsulates our research question.

Therefore, under the assumption of the null, the sampling distribution is the null distribution, meaning that it’s centered at 0.5. All work we do with the normal model, including checking conditions, must use the null model with \(p_{alive}= 0.5\).

That’s also why the numbers don’t have to be whole numbers. If the null states that of the 69 patients, 50% are expected to survive, then we expect 50% of 69, or 34.5, to survive. Of course, you can’t have half of a survivor. But these are not actual survivors. Rather, they are the expected number of survivors in a group of 69 patients on average under the assumption of the null.

15.8 Mechanics

15.8.1 Compute the test statistic.

alive_prop <- heart_transplant2 |>
  specify(response = survived, success = "alive") |>
  calculate(stat = "prop")
alive_prop

We’ll also compute the corresponding z score.

alive_z <- heart_transplant2 |>
  specify(response = survived, success = "alive") |>
  hypothesize(null = "point", p = 0.5) |>
  calculate(stat = "z")
alive_z

Commentary: The sample proportion code is straightforward and we’ve seen it before. To get the z score, we also have to tell infer what the null hypothesis is so that it knows where the center of our normal distribution will be. In the hypothesize function, we tell infer to use a “point” null hypothesis with p = 0.5. All this means is that the null is a specific point: 0.5. (Contrast this to hypothesis tests with two variables when we had null = "independence".)

We can confirm the calculation of the z score manually. It’s easiest to compute the standard error first. Recall that the standard error is

\[ SE = \sqrt{\frac{p_{alive}(1 - p_{alive})}{n}} = \sqrt{\frac{0.5(1 - 0.5)}{69}} \]

Remember that are working under the assumption of the null hypothesis. This means that we use \(p_{alive} = 0.5\) everywhere in the formula for the standard error.

We can do the math in R and store our result as SE.

SE <- sqrt(0.5*(1 - 0.5)/69)
SE

[1] 0.06019293

Then our z score is

\[ z = \frac{(\hat{p}_{alive} - p_{alive})}{SE} = \frac{(\hat{p}_{alive} - p_{alive})}{\sqrt{\frac{p_{alive} (1 - p_{alive})}{n}}} = \frac{(0.348 - 0.5)}{\sqrt{\frac{0.5 (1 - 0.5)}{69}}} = -2.53. \]

Using the values of alive_prop and SE:

z <- (alive_prop - 0.5)/SE
z

Both the sample proportion \(\hat{p}_{alive}\) (stored above as alive_prop) and the corresponding z-score can be considered the “test statistic”. If we use \(\hat{p}_{alive}\) as the test statistic, then we’re considering the null model to be

\[ N\left(0.5, \sqrt{\frac{0.5 (1 - 0.5)}{69}}\right). \]

If we use z as the test statistic, then we’re considering the null model to be the standard normal model:

\[ N(0, 1). \]

The standard normal model is more intuitive and easier to work with, both conceptually and in R. Generally, then, we will consider z as the test statistic so that we can consider our null model to be the standard normal model. For example, knowing that our test statistic is two and a half standard deviations to the left of the null value already tells us a lot. We can anticipate a small P-value leading to rejection of the null. Nevertheless, for this type of hypothesis test, we’ll compute both in this section of the rubric.

15.8.2 Report the test statistic in context (when possible).

The test statistic is 0.3478261. In other words, 34.7826087% of heart transplant recipients were alive at the end of the study.

The z score is -2.5281029. The proportion of survivors is about 2.5 standard errors below the null value.

Commentary: It’s useful to report both versions of the test statistic. One tells us the value from the data. The other tells us how many standard deviations that value lies from the null value. Both are contextually meaningful.

15.8.3 Plot the null distribution.

alive_test <- heart_transplant2 |>
  specify(response = survived, success = "alive") |>
  hypothesize(null = "point", p = 0.5) |>
  assume(distribution = "z")
alive_test

A Z distribution.

alive_test |>
  visualize() +
  shade_p_value(obs_stat = alive_z, direction = "less")

Commentary: be sure to use alive_z here (and not alive_prop). The infer package assumes a standard normal model, centered at 0 with standard deviation 1.

In past chapters, we have used the generate verb to get many repetitions (usually 1000) of some kind of random process to simulate the sampling distribution model. In this chapter, we have used the verb assume instead to assume that the sampling distribution is a normal model. As long as the conditions hold, this is a reasonable assumption. This also means that we don’t have to use set.seed as there is no random process to reproduce.

Compare the graph above to what we would see if we simulated the sampling distribution. (Now we do need set.seed!)

set.seed(6789)
alive_test_draw <- heart_transplant2 |>
  specify(response = survived, success = "alive") |>
  hypothesize(null = "point", p = 0.5) |>
  generate(reps = 1000, type = "draw") |>
  calculate(stat = "prop")
alive_test_draw

alive_test_draw |>
  visualize() +
  shade_p_value(obs_stat = alive_prop, direction = "less")

This is essentially the same picture, although the model above is centered on the null value 0.5 instead of the z score of 0. (This also means that the obs_stat had to be the sample proportion alive_prop and not the z score alive_z, but we’re only using alive_prop and simulations here to illustrate the point that the normal model and the simulation result in essentially the same model.)

15.8.4 Calculate the P-value.

alive_test_p <- alive_test |>
  get_p_value(obs_stat = alive_z, direction = "less")
alive_test_p

Commentary:

As before, there are two test statistics floating around: alive_prop and alive_z. Be sure to use alive_z here!

We can compare this to the P-value we get from simulating random draws:

alive_test_draw |>
  get_p_value(obs_stat = alive_prop, direction = "less")

The values are not exactly the same. And a new simulation with a different seed would likely give another slightly different P-value. The takeaway here is that the P-value itself has some uncertainty, so you should never take the value too seriously.

15.8.5 Interpret the P-value as a probability given the null.

The P-value is 0.005734. If there were truly a 50% chance of survival among heart transplant patients, there would only be a 0.5734037% chance of seeing data at least as extreme as we saw.

15.9 Conclusion

15.9.1 State the statistical conclusion.

We reject the null hypothesis.

15.9.2 State (but do not overstate) a contextually meaningful conclusion.

We have sufficient evidence that heart transplant recipients have less than a 50% chance of survival.

15.9.3 Express reservations or uncertainty about the generalizability of the conclusion.

Because we know nearly nothing about the provenance of the data, it’s hard to generalize the conclusion. We know the data is from 1974, so it’s also very likely that survival rates for heart transplant patients then are not the same as they are today. The most we could hope for is that the Stanford data was representative for heart transplant patients in 1974. Our sample size (69) is also quite small.

15.9.4 Identify the possibility of either a Type I or Type II error and state what making such an error means in the context of the hypotheses.

As we rejected the null, we run the risk of making a Type I error. It is possible that the null is true and that there is a 50% chance of survival for these patients, but we got an unusual sample that appears to have a much smaller chance of survival.

15.10 Confidence interval

15.10.1 Check the relevant conditions to ensure that model assumptions are met.

• Random
  • Same as above.
• 10%
  • Same as above.
• Success/failure
  • There were 24 patients who survived and 45 who died in our sample. Both are larger than 10.

Commentary: In the “Confidence interval” section of the rubric, there is no need to recheck conditions that have already been checked. The sample has not changed; if it met the “Random” and “10%” conditions before, it will meet them now.

So why recheck the success/failure condition?

Keep in mind that in a hypothesis test, we temporarily assume the null is true. The null states that \(p = 0.5\) and the resulting null distribution is, therefore, centered at \(p = 0.5\). The success/failure condition is a condition that applies to the normal model we’re using, and for a hypothesis test, that’s the null model.

By contrast, a confidence interval is making no assumption about the “true” value of \(p\). The inferential goal of a confidence interval is to try to capture the true value of \(p\), so we certainly cannot make any assumptions about it.

So what can we do to check the success/failure condition without a “true” value for \(p\)? Whenever we are lacking a true population parameter, the best we can do is substitute our best guess for the value of that parameter. And our best guess for the true population proportion \(p\) is our sample proportion \(\hat{p}\).

Instead of \(np\) and \(n(1 - p)\), then, we can calculate \(n\hat{p}\) and \(n(1 - \hat{p})\):

\[ n\hat{p} = 69 * 0.3478261 = 24 \]

\[ n(1 - \hat{p}) = 69 * (1 - 0.3478261) = 45 \]

But 24 and 45 are the actual number of successes and failures from the data! This makes sense: if you multiply the sample size (69) by the proportion of people who survived the heart transplant, you get the number of people who survived the heart transplant.

So, for confidence intervals, we simply report the number of successes and failures in the data and check that each is at least 10.

15.10.2 Calculate and graph the confidence interval.

alive_ci <- alive_test |>
  get_confidence_interval(point_estimate = alive_prop, level = 0.95)
alive_ci

alive_test |>
  visualize() +
  shade_confidence_interval(endpoints = alive_ci)

Commentary: when we use a theoretical normal distribution, we have to compute the confidence interval a different way.

When we bootstrapped, we had many repetitions of a process that resulted in a sampling distribution. From all those, we could find the 2.5th percentile and the 97.5th percentile. Although we let the computer do it for us, the process is straightforward enough that we could do it by hand if we needed to. Just put all 1000 bootstrapped values in order, then go to the 25th and 975th position in the list.

We don’t have a list of 1000 values when we use an abstract curve to represent our sampling distribution. Nevertheless, we can find the 2.5th percentile and the 97.5th percentile using the area under the normal curve as we saw in the last two chapters. We can do this “manually” with the qdist command, but we need the standard error first.

Didn’t we calculate this earlier?

\[ SE = \sqrt{\frac{p_{alive}(1 - p_{alive})}{n}} = \sqrt{\frac{0.5(1 - 0.5)}{69}} \]

Well…sort of. The value of \(p_{alive}\) here is the value of the null hypothesis from the hypothesis test above. However, the hypothesis test is done. For a confidence interval, we have no information about any “null” value. There is no null anymore. It’s irrelevant.

So what is the standard error for a confidence interval? Since we don’t have \(p_{alive}\), the best we can do is replace it with \(\hat{p}_{alive}\):

\[ SE = \sqrt{\frac{\hat{p}_{alive} (1 - \hat{p}_{alive})}{n}} = \sqrt{\frac{0.3478261 (1 - 0.3478261 )}{69}}. \]

We can let R do the heavy lifting here:

SE2 <- sqrt(alive_prop * (1 - alive_prop) / 69)
SE2

And now this number can go into qdist as our standard deviation:

qdist("norm", p = c(0.025, 0.975), mean = 0.3478261, sd = 0.05733743, plot = FALSE)

[1] 0.2354468 0.4602054

The numbers above are identical to the ones computed by the infer commands.

15.10.3 State (but do not overstate) a contextually meaningful interpretation.

We are 95% confident that the true percentage of heart transplant recipients who survive is captured in the interval (23.5446784%, 46.020539%).

Commentary: Note that when we state our contextually meaningful conclusion, we also convert the decimal proportions to percentages. Humans like percentages a lot better.

15.10.4 If running a two-sided test, explain how the confidence interval reinforces the conclusion of the hypothesis test.

We are not running a two-sided test, so this step is not applicable.

15.10.5 Comment on the effect size and the practical significance of the result.

We estimate that between 24% and 46% of patients who received heart transplants survived. Even the most optimistic estimate is still below the null value of 50%. This is a significant difference and tells us that it’s not even close to a “coin flip.” Although we are told that survival rates are better when receiving a heart transplant versus not receiving one, there is a substantial risk of death, even with a heart transplant.

Commentary: up to this point in the course, we had scenarios in which we had run hypothesis tests but not confidence intervals, or confidence intervals but not hypothesis tests. This is the first time we’ve run both, so we are now in a position to opine about effect size. The idea is to compare the range of values from the confidence interval to the null value. What is the worst-case scenario? What is the best-case scenario? In either event, is the magnitude of the difference clinically important to these patients? A 1% difference might not be, but a 10% difference might be.

It’s not enough just to reject the null hypothesis and calculate a confidence interval. We want to indicate whether the data makes a strong case about the research question. A statistically discernible result alone (a P-value less than 0.05) will tell us only that we can confidently reject the null. But that cannot tell us if the result in meaningful in a real-world setting.

15.11 Your turn

Follow the rubric to answer the following research question:

Some heart transplant candidates have already had a prior surgery. Use the variable prior in the heart_transplant data set to determine if fewer than 50% of patients have had a prior surgery. (To be clear, you are being asked to perform a one-sided test again.) Be sure to use the full heart_transplant data, not the modified heart_transplant2 from the previous example.

The rubric outline is reproduced below. You may refer to the worked example above and modify it accordingly. Remember to strip out all the commentary. That is just exposition for your benefit in understanding the steps, but is not meant to form part of the formal inference process.

Another word of warning: the copy/paste process is not a substitute for your brain. You will often need to modify more than just the names of the tibbles and variables to adapt the worked examples to your own work. For example, if you run a two-sided test instead of a one-sided test, there are a few places that have to be adjusted accordingly. Understanding the sampling distribution model and the computation of the P-value goes a long way toward understanding the changes that must be made. Do not blindly copy and paste code without understanding what it does. And you should never copy and paste text. All the sentences and paragraphs you write are expressions of your own analysis. They must reflect your own understanding of the inferential process.

Also, so that your answers here don’t mess up the code chunks above, use new variable names everywhere. In particular, you should use prior_test(instead of alive_test) to store the results of your hypothesis test. Make other corresponding changes as necessary, like prior_test_p instead of alive_test_p, for example.

Exploratory data analysis

Use data documentation (help files, code books, Google, etc.) to determine as much as possible about the data provenance and structure.

Please write up your answer here.

# Add code here to print the data

# Add code here to glimpse the variables

Prepare the data for analysis.

# Add code here to prepare the data for analysis.

Make tables or plots to explore the data visually.

# Add code here to make tables or plots.

Hypotheses

Identify the sample (or samples) and a reasonable population (or populations) of interest.

[Remember that you are using the full heart_transplant data, so your sample size should be larger here than in the example above.]

Please write up your answer here.

Express the null and alternative hypotheses as contextually meaningful full sentences.

\(H_{0}:\) Null hypothesis goes here.

\(H_{A}:\) Alternative hypothesis goes here.

Express the null and alternative hypotheses in symbols (when possible).

\(H_{0}: math\)

\(H_{A}: math\)

Model

Identify the sampling distribution model.

Please write up your answer here.

Check the relevant conditions to ensure that model assumptions are met.

[Remember that you are using the full heart_transplant data, so the number of successes and failures will be different here than in the example above.]

Please write up your answer here. (Some conditions may require R code as well.)

Mechanics

[Be sure to use heart_transplant everywhere and not heart_transplant2!]

Compute the test statistic.

# Add code here to compute the test statistic as a proportion.

# Add code here to compute the test statistic as a z score.

Report the test statistic in context (when possible).

Please write up your answer here.

Plot the null distribution.

[Be sure to use the z score here, not the sample proportion!]

# Add code here to generate the null distribution.

# Add code here to plot the null distribution.

Calculate the P-value.

# Add code here to calculate the P-value.

Interpret the P-value as a probability given the null.

Please write up your answer here.

Conclusion

State the statistical conclusion.

Please write up your answer here.

State (but do not overstate) a contextually meaningful conclusion.

Please write up your answer here.

Express reservations or uncertainty about the generalizability of the conclusion.

Please write up your answer here.

Identify the possibility of either a Type I or Type II error and state what making such an error means in the context of the hypotheses.

Please write up your answer here.

Confidence interval

Check the relevant conditions to ensure that model assumptions are met.

Please write up your answer here. (Some conditions may require R code as well.)

Calculate the confidence interval.

# Add code here to calculate the confidence interval.

State (but do not overstate) a contextually meaningful interpretation.

Please write up your answer here.

If running a two-sided test, explain how the confidence interval reinforces the conclusion of the hypothesis test. [Not always applicable.]

Please write up your answer here.

When comparing two groups, comment on the effect size and the practical significance of the result.

Please write up your answer here.

15.12 Conclusion

When certain conditions are met, we can use a theoretical normal model—a perfectly symmetric bell curve—as a sampling distribution model in hypothesis testing. Because this does not require drawing many samples, it is faster and cleaner than simulation. Of course, on modern computing devices, drawing even thousands of simulated samples is not very time consuming, and the code we write doesn’t really change much. Given the additional success/failure condition that has to met, it’s worth considering the pros and cons of using a normal model instead of simulating the sampling distribution. Similarly, confidence intervals can be obtained directly from the percentiles of the normal model without the need to obtain bootstrapped samples.

15.12.1 Preparing and submitting your assignment

1. From the “Run” menu, select “Restart R and Run All Chunks”.
2. Deal with any code errors that crop up. Repeat steps 1–2 until there are no more code errors.
3. Spell check your document by clicking the icon with “ABC” and a check mark.
4. Hit the “Render” button one last time to generate the final draft of the HTML file. (If there are errors here, you may need to go back and fix broken inline code or other markdown issues.)
5. Proofread the HTML file carefully. If there are errors, go back and fix them, then repeat steps 1–5 again.

If you have completed this chapter as part of a statistics course, follow the directions you receive from your professor to submit your assignment.